Si supponga che due sistemi di riferimento si muovano, l'uno rispetto all'altro,
di moto rettilineo ed uniforme.
In questo caso, se la velocità relativa dei due sistemi è significativamente alta, prossima a quella della luce,
un osservatore in uno dei due sistemi di riferimento, vedrà le lunghezze dell'altro sistema,
nella direzione del moto, contratte.
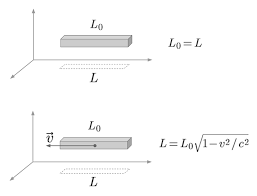
Indicando con L la lunghezza propria di un oggetto, vale a dire la lunghezza misurata da un osservatore
solidale col sistema di riferimento in cui si trova l'oggetto, e con L0 la lunghezza, contratta, quella misurata
da un osservatore che si trova nel sistema di riferimento che si muove di moto rettilineo ed uniforme
rispetto a quello in cui si trova l'oggetto, le grandezze L ed L0 saranno legate dalla relazione
L0 = L/γ
dove γ=1/√(1- (v/c)2)
DA questa relazione γ=1/√(1- (v/c)2), si evince che, quando la velocità v si avvicina a c
il rapporto v/c tende ad 1, rimanendo un pò più piccolo di uno. Pertanto, il denomminatore della relazione prima scritta
tende a zero, rimanendo leggermente più grande di zero. L'inverso del denominatore, tenderà a più infinito
In ultima analisi, quando v --> c, il fattore γ tende a ∞ Di conseguenza la quantità L0 tenderà a zero
Immaginiamo che un aereo stia atterrando su una pista ad una velocità prossima a quella della luce, la lunghezza della pista apparirebbe
contratta, al pilota. Al limite, quando v -->c , il pilota dell'aereo vedrebbe la pista puntiforme!
AGGIORNA LA PAGINA FRA UN CALCOLO ED IL SUCCESSIVO
Scegli l'unità di misura della velocità relativa fra i due sistemi di riferimento
quello "fermo" e quello in moto
scegli:
1 per km/s
2 per km/h
3 per m/s
scelta
Introduci il valore numerico della velocità relativa
velocità relativa
Breve premessa: la lunghezza propria di un oggetto è quella misurata da un osservatore che si trova
sullo stesso sistema di riferimento dell'oggetto. Mentre la lunghezza contratta è quella misurata dall'osservatore che si trova nel
sistema di riferimento in moto relativo.
Introduci la lunghezza propria di un certo oggetto nella direzione del moto
Esempio: un per "chilometro e settecento metri", segna 1 nella casella dei km
e 700 nella casella dei metri.
Per 600 m, segna 0 nella casella dei chilometri e 600 nella casella dei metri
km + m
Hai scelto
velocità_relativa = ... ...
Nel tuo caso il fattore gamma sarà:
gamma = ...
Per l'osservatore in moto, la lunghezza propria dell'oggetto, che si trova nell'altro sistema di
riferimento, apparirà contratta e sarà pari a:
lunghezza_contratta = ... km + ... m +
... cm